Berhubung dari postingan vektor (SMA)
banyak sekali sobat yang menanyakan tentang bagaimana menjumlahkan dan
mengurangkan dua vektor atau lebih, kali ini kami coba membahas khusus
tentang operasi penjumlahan dan pengurangan vektor. Untuk melakukan
operasi penjumlahan atau pengurangan terhadap dua vektor atau lebih,
sobat hitung bisa memakai 3 cara tau metode yaitu
1. Metode Jajar Genjang
Metode jajar genjang
adalah metode menentukan resultan vektor dengan memodifikasi titik
himpit dan arah vektor. Dua vektor dengan pangkal berimpit digambar
sebagai dus isisi yang berdekatan dari sebuah bangun jajar genjang, maka
jumlah vektornya adalah sama dengan vektor diagonal yang pangkalnya
sama dengan pangkal kedua vektor yang berhimpit tadi. Ilustrasinya.
Dua vektor (Vektor A dan Vektor B) sebelumnya terpisah, kemudian kita
himpitkan pangkalnya sehingga membentuk sudut α sehingga masing-masing
vektor menjadi sisi-sisi yang berdekatan dari sebuah jajar genjang
seperti gambar di bawah ini

Resultan vektor yang terbentuk akan berada di antara vektor A dan B dan membentuk sudut α1 dengan vektor A dan sudut α2 dengan vektor B.
Rumus Penjumlahan Vektor
Pada metode jajar genjang resultan dua vektor dapat dicari dengan rumus
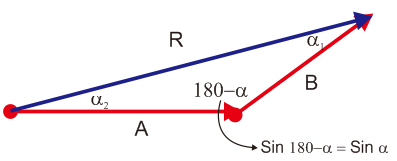
Sekarang, yang sering ditanyakan sobat adalah bagaimana mencari sudut resultannya? Untuk mencari Sudut resultan bisa menggunakan aturan sinus pada segitiga.
Rumus Pengurangan Vektor
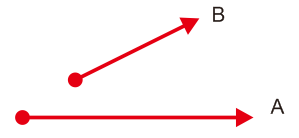
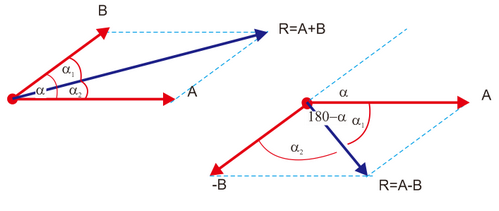
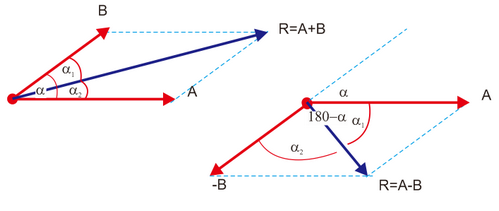
Untuk pengurangan vektor prinsipnya sama saja. Tidak perlu bingung. Misal ada 2 buah vektor berhimpit seperti gambat dibawah ini
Jika dibuat pengurangan vektor A-B maka
sobat cukup merubah arah vektor B sehingga ujung jadi pangkal dan
pangkal jadi ujung. Perhatikan gambar di atas.
Rumusnya pun sama dengan rumus
Penjumlahan tapi dengn sudut yang berbeda. Sekarang sudut yang dibentuk
antara vektor A dan B adalah 180º – α. Karena di kuadran dua nilai
cosinus adalah negatif maka Cos (180º-α) = – cos α
Ada dua buah vektor yaitu Vektor A dan Vektor B yang masing-masing
besarnya 20 dan 10 satuan. Jika sudut antara kedua vektor tersebut
adalah 60º tentukan besar resultan vektor A-B dan sudut dari Resultan
tersebut.
Jawab.
Besarnya sudut apit antara vektor A dan -B = 180º – 60º = 120º
Cos 120º = -1/2
Besarnya sudut apit antara vektor A dan -B = 180º – 60º = 120º
Cos 120º = -1/2
2. Metode Segitiga
Metode ini mirip dengan metode jajar
genjang. Penjumlahan atau selisih dua buah vektor dapat diselesaikan
menggunakan metode segitiga dengan langkah-langkah
a. Pangkal dari Vektor Keuda diletakkan pada ujung vektor pertama.b. Reasul hasil penjumlahan digambarkan dari pangkal vektor pertama ke ujung vektor kedua.
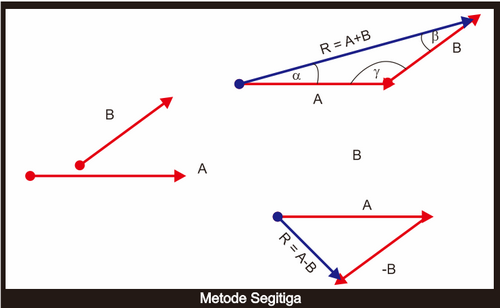
Rumus nya
 γ = sudut apit atau sudut terkecil yang debentuk oleh vektor A dan B
γ = sudut apit atau sudut terkecil yang debentuk oleh vektor A dan B3. Metode Penguraian Vektor atau Vektor Komponen
Alternatif lain menentukan resultan
vektor bisa dengan menguraikan setiap vektor ke komponen x dan y nya.
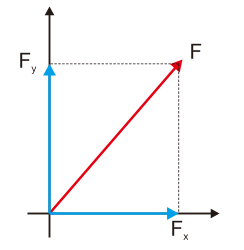
Contonya sebagai berikut, ada sebuah vektor dengan panjang 20 satuan dan
membentuk sudut 60º dengan sumbu x maka cara penguraiannya
Fx = F cos α
Fy = F sin α
Fx = 20 cos 60º = 20 0,5 = 10
Fy = 20 sin 60º = 20 0,5√3 = 10 √3
Fy = 20 sin 60º = 20 0,5√3 = 10 √3
Untuk rumus resultan vektornya menggunakan
Untuk mencari sudutnya menggunakan aturan tagen dimana
Ada dua buah vektor gaya F1 dan F2 bertitik tangakap di 0 seperti gambar di bawah ini. Tentukan resultan vektor tersebut dan sudutnya dari sumbu x positif.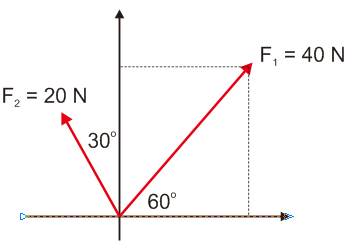
Jawab
Sudut antara vektor F1 dan sumbu x positif adalah θ = 60º, maka
F1x = F1 cos θ = 40 (0,5) = 20
F1y = F1 sin θ = 40 (0,5 √3) = 20 √3
Sudut antara vektor F2 dengan sumbu X positif adalah 90º + 30º = 120º maka
F2x = F2 cos 120 = 20 (-0,5) = -10
F2y = F2 sin 120 = 20 (0,5 √3) = 10√3
Fx total = F1x + F2x = 20 – 10 = 10
Fy total = F1y + F2y = 20 √3 + 10√3 = 30√3
Tan α = Fy / Fx
Tan α = 30√3/10 = 3√3
F2x = F2 cos 120 = 20 (-0,5) = -10
F2y = F2 sin 120 = 20 (0,5 √3) = 10√3
Fx total = F1x + F2x = 20 – 10 = 10
Fy total = F1y + F2y = 20 √3 + 10√3 = 30√3
Tan α = Fy / Fx
Tan α = 30√3/10 = 3√3
α = arc tan 3√3 = 79,1º (sobat bisa menggunakan rumus excel =degrees(atan(3√3))
Jadi resultan dari penjumlahan vektor F1 dan F2 mempunyai sudut 79,1º dari sumbu x positif





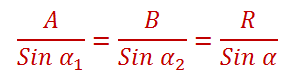
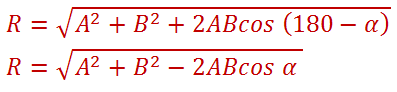
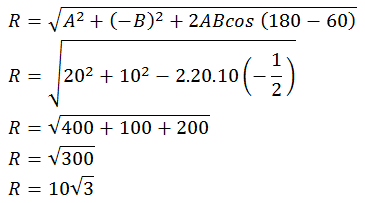

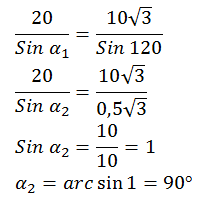
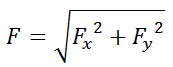
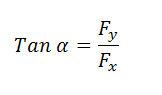





0 komentar:
Posting Komentar