Kumpulan Contoh Soal Logika Matematika – Spesial
buat latihan sobat hitung berikut kami sajikan beberapa contoh soal
logika matematika yang bisa sobat jadikan bahan latihan belajar
mempersiapkan ujian nasional yang tinggal 7 bulan lagi. Soal-soal ini
untuk melengkapi postingan soal logika matematika
sebelumnya. Sebelum mengerjakan soal ada baiknya sobat review ulang
dengan membaca buku pelajaran dari sekolah. Yakin jika sobat mau belajar
sungguh-sungguh pasti semua sola di bawah ini bisa dilibas tanpa ampun.
Hehehehe. Let’s check this Ouuuut.. 
Kumpulan Soal Logika Matematika
- Jika sobat diberikan pernyataan ( p ∨ ~q), maka konvers dari penyataan tersebut adalah
a. p → (~p ∨q) c. p → (p∨~q) e. p → (~p∧~q) b. p → (p ∧~q) d. p → (~p∨~q) - Jika p bernilai salah, q benar, sedangkan ~p dan ~ q merupakan
ingkaran dari p dan q, maka pernyataan di bawah ini yang benar adalah:
a. ~p ⇒ ~q bernilai benar c. p ⇒q bernilai salah e. p ⇒q bernilai benar b. ~q ⇒ ~p bernilai salah d. ~p ⇒q bernilai salah - Pernyataan (p∨q) ⇒ bernilai salah jika
a. p benar dan q benar c. p salah q benar e. bukan semuanya b. p benar q salah d. p salah q salah - Jika ada sebuah pernyataan majemuk : Jika hari hujan maka jalan-jalan di jakarta akan banjir ekivalen dengan pernyataan
a. Hari hujan dan jalan-jalan di Jakarta Banjir b. Jika jalan-jalan di Jakarta banjir maka hari hujan c. Hari tidak hujan dan jalan-jalan di Jakarta tidak banjir. d. Jika hari tidak hujan maka jalan-jalan di jakarta tidak banjir - Ingkaran dari pernyataan “Semua peserta tes bedoa sebelum mengerjakan soal”
a. Semua peserta tes tidak berdoa sebelum mengerjakan tugas b. Beberapa peserta tes berdoa sebelum mengerjakan soal c. Beberapa peserta tes tidak beroa sebelum mengerjakan soal d. Beberapa peserta tes berdoa setelah mengerjakan soal - Pernytaan : “Jika hari gelap maka lampu dinyalakan” ekivalen dengan pernyataan
a. Jika lampu tidak dinyalakan maka hari tidak gelap b. Jika hari gelap maka lampu tidak dinyalakan c. Jika tidak gelap maka lampu tidak dinyalakan d. Jika hari tidak gelap maka lampu dinyalakan - Jika sobat diberika pernyataan “Jika semua siswa menyukai matematika maka guru senang mengajar“. Konta posisi dari pernyataan tersebut adalah …
a. Jika guru senang mengajar pasti ada siswa yang tidak suka matematika b. Jika tidak semua siswa suka matematika maka guru tidak senang mengajar c. Jika guru tidak senang mengajar maka ada siswa yang suka matematika d. Jika guru tidak senang mengajar maka ada siswa yang tidak suka matematika - Ingkaran dari pernyataan √15 < 4 jika dan hanya jika sin 30o < sin 45o adalah
a. √15 <= 4 jika dan hanya jika sin 30o < sin 45o b. √15 < 4 jika dan hanya jika sin 30o > sin 45o c. √15 >= 4 jika dan hanya jika sin 30o > sin 45o d. √15 < 4 jika dan hanya jika sin 30o >= sin 45o e. √15 < 4 jika dan hanya jika sin 30o = sin 45o - Kontraposisi dan implikasi dari penyataan “Jika saya lulus ujian saya akan puasa nazar”
a. Jika saya puasa nazar maka saya lulus ujian b. Jika saya lulus ujian, saya tidak akan puasa nazar c. Jika saya tidak lulus ujian maka saya tidak puasa nazar d. Jika saya tidak puasa nazar maka saya tidak lulus ujian - Ingkaran dari pernyataan (p ∧ q) → q
a. (p∧q) ∧ ~q c. ~(p∧q) ∧ q e. (p∧q) ∨ ~q b. (p∧q) ∧ q d. (~p∨~q) ∨ ~q - “Jika binatang itu kuda, maka binantang itu berkaki empat”
Ternyata binatang itu tidak berkaki empat
Kesimpulannya adalah …
a. binatang itu kuda b. binatang itu bebek c. binatang itu pasti bukan ayam d. binatang itu bukan kuda d. pasti itu kudanil - Sobat hitung diberika pernyataan “Hanya jika sobat bekerja keras, sobat akan sukses”
jika ternyata sobat selalu bekerja keras, maka pernyataan berikut yang benar adalah …
a. Sobat selalu sukses b. Sobat tidak pernah sukses c. Kamu kadang-kadang sukses d. Tidak ada yang dapat disimpulkan e. Bukan semuanya - Diketahui argumentasi
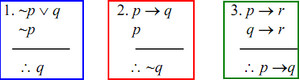diantara argumentasi logika matematika di atas manakah yang sah adalah
a. 1,2,4 saja c. 1 dan 3 e. 3 saja b. 1 dan 2 d. 2 saja - Pernyataan “Jika dia merah, maka dia adalah darah”
Pernyataan berikut yang benar adalah …
I. Dia tidak merah, maka dia bukan darah
II. Dia adalah darah, maka dia adalah merah
III. Dia bukan darah, maka dia tidak merah
a. hanya I c. hanya III e. II dan III b. hanya II d. I dan III - Pernyataan : “Jika laba tinggi maka karyawan sejahtera” mempunyai invers yaitu
a. Jika laba tinggi maka karyawan tidak sejahtera b. Jika laba rendah maka karyawan tidak sejahtera c. Jika laba rendah maka karyawan sejahtera d. Jika laba tinggi maka karyawan sejahtera e. Jika laba tinggi maka karyawan tidak sejahtera - Kontraposisi pernyataan “Jika saya mengantuk saya akan tidur” adalah
a. Jika tidak mengantuk, saya tidak tidur b. Saya mengantuk, saya nonton liga inggris c. Saya tidak mengantuk dan saya tidak tidur d. Saya tidak tidur, saya bermain ping pong e. Jika saya tidak tidur maka saya tidak mengantuk - Ingkaran dari pernyataan “Jika sobat rajin belajar maka sobat tidak lulus USM STAN” adalah
a. Sobat rajin belajar dan sobat tidak lulus USM STAN b. Sobat rajin belajar dan sobat lulus USM STAN c. Sobat rajin belajar atau sobat lulusUSM STAN d. Sobat tidak rajin belajar dan sobat tidak lulus USM STAN - a, b, c, dan d adalah pernyataan. Jika pernyataan-pernyataan berikut bernilai benar
p ∧ q
p ⇔ r
r ⇔ s
maka pernyataan berikut yang benar adalah
a. p∨q c. p ⇒q b. ~ p∨q d. -p⇒-s - Ada 2 pernyataan:
I. Beberapa bilangan bukan bilangan prima
II. Tidak ada bilangan prima yang merupakan bilangan kuadrat
Jika beberapa berarti “Paling sedikit sat”, maka dari pernyataan I dan II dapat disimpulkan
a. Beberapa bilangan dalah bilangan kuadrat b. Beberapa bilangan kuadrat bukan bilangan c. Beberapa bilangan bukan bilangan kuadrat d. Tidak ada bilangan yang bilangan kuadrat e. Tidak satupun yang di atas merupakan kesimpulan pernyataan I dan II - Perhatikan ungkapan: “Semua pemain tinju berbadan kekar.” Negasi ungkapan tersebut adalah
a. Tidak ada pemain tinju yang erbadan kekar b. Beberapa pemain tinju berbadan kekar c. Beberapa pemain tinju berbadan biasa d. Semua pemain tinju berbadan biasaa d. Tidak ada pemain tinju yang berbadan biasa. - Pernyataan “Jika Ririn lulus ujian, maka ririn akan langsung akad nikah” senilai dengan …
-
Hwaa lumayan banyak dan aga membingungkan. Tapi buat sobat yang mau berusaha pasti bisa menemukan jawaban dari tiap contoh soal logika matematika di atas. Selama bejuang.a. Jika ririn lulus, maka ririn akan akad nikah b. Jika ririn tidak lulus ujian, maka ririn akan akad nikah c. Jika ririn tidak lulus ujian, maka ririn tidak akad nikah d. Jika ririn tidak akad nikah, maka ririn tidak lulus ujian
0 komentar:
Posting Komentar